
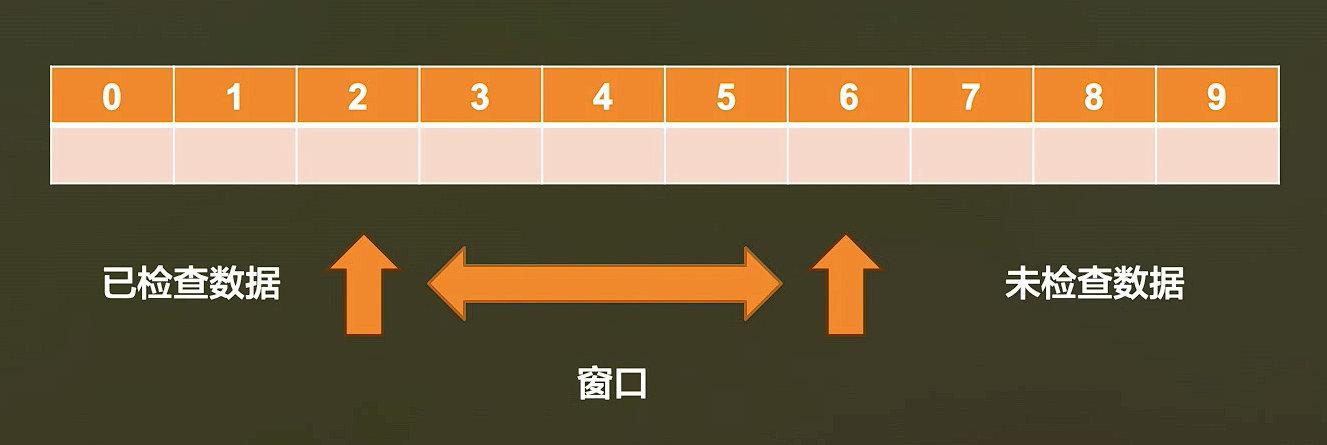
1.无重复字符的最长子串

解题思路
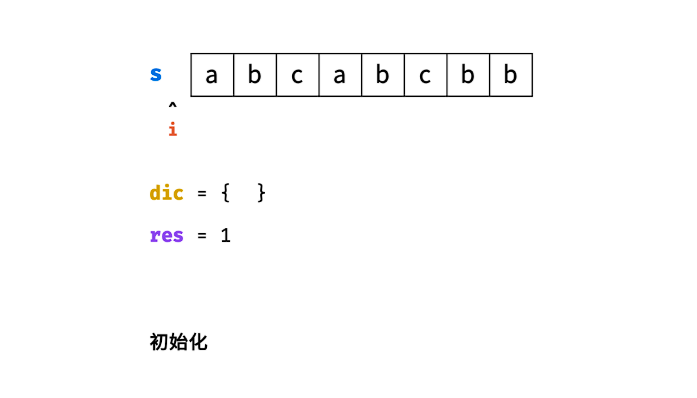
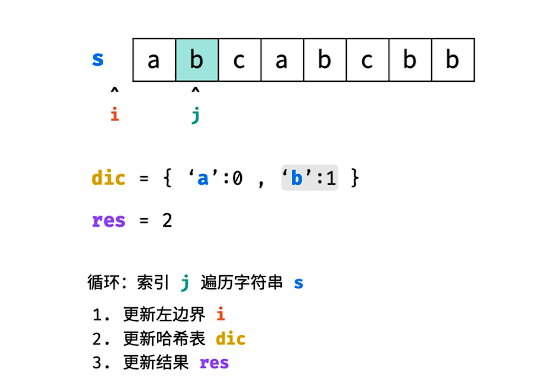
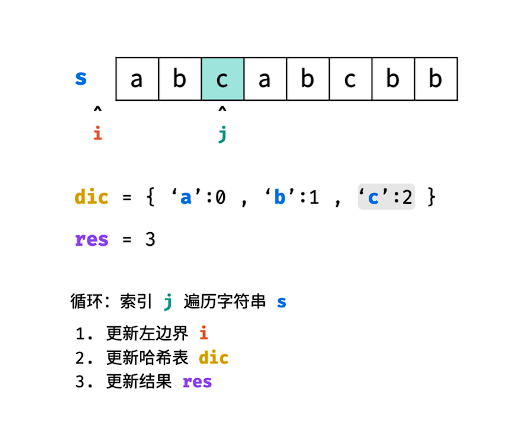
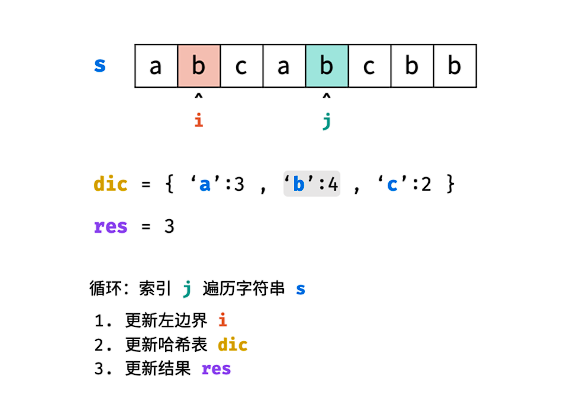
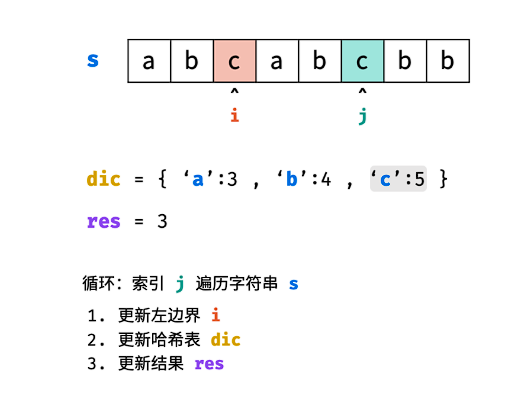
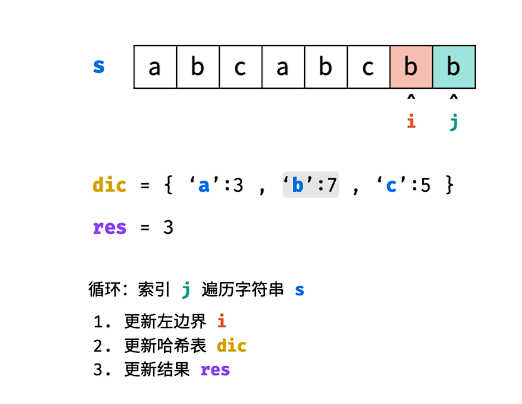
哈希表 dic 统计: 指针 j 遍历字符 s ,哈希表统计字符 s[j] 最后一次出现的索引 。
更新左指针 i : 根据上轮左指针 i 和 dic[s[j]] ,每轮更新左边界 i ,保证区间 [i+1,j] 内无重复字符且最大。
i=max(dic[s[j]],i)
更新结果 res : 取上轮 res 和本轮双指针区间 [i+1,j] 的宽度(即 j−i )中的最大值。
res=max(res,j−i)




代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public int lengthOfLongestSubstring(String s) {
Map<Character,Integer> map = new HashMap<>();
int i = -1,res = 0,lens = s.length();
for (int j = 0; j < lens; j++) {
if(map.containsKey(s.charAt(j))){
i = Math.max(i,map.get(s.charAt(j)));// 更新左指针 i
}
map.put(s.charAt(j),j);// 哈希表记录
res = Math.max(res,j - i);// 更新结果
}
return res;
}
}
复杂度分析
-
时间复杂度 O(N) : 其中 N 为字符串长度,动态规划需遍历计算 d p 列表。
-
空间复杂度 O(1) : 字符的 ASCII 码范围为 0 ~ 127 ,哈希表 dic 最多使用 O(128)=O(1) 大小的额外空间。
2.找到字符串中所有字母异位词

解题思路
枚举 s 的所有长为 n 的子串 s′,如果 s′ 的每种字母的出现次数,和 p 的每种字母的出现次数都相同,那么 s′ 是 p 的异位词。
本题维护长为 n 的子串 s′ 的每种字母的出现次数。如果 s′ 的每种字母的出现次数,和 p 的每种字母的出现次数都相同,那么 s′ 是 p 的异位词,把 s′ 左端点下标加入答案。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public List<Integer> findAnagrams(String s, String p) {
List<Integer> res = new ArrayList<>();
int[] cntP = new int[26];// 统计 p 的每种字母的出现次数
int[] cntS = new int[26];// 统计 s 的长为 p.length() 的子串 s' 的每种字母的出现次数
for(char c : p.toCharArray()){
cntP[c - 'a']++;// 统计 p 的字母个数
}
for (int right = 0; right < s.length(); right++) {
cntS[s.charAt(right) - 'a']++;// 右端点字母进入窗口
int left = right - p.length() + 1;
if(left < 0){// 窗口长度不足 p.length()
continue;
}
if(Arrays.equals(cntP,cntS)){
res.add(left); //s' 左端点下标加入答案
}
cntS[s.charAt(left) - 'a']--;// 左端点字母离开窗口
}
return res;
}
}
复杂度分析
-
时间复杂度:O(∣Σ∣m+n),其中 m 是 s 的长度,n 是 p 的长度,∣Σ∣=26 是字符集合的大小
-
空间复杂度:O(∣Σ∣)。返回值不计入
总结

