
1.移动零

解题思路
两次遍历 我们创建两个指针 i 和 j,第一次遍历的时候指针 j 用来记录当前有多少 非 0 元素。即遍历的时候每遇到一个 非 0 元素就将其往数组左边挪,第一次遍历完后,j 指针的下标就指向了最后一个 非 0 元素下标。 第二次遍历的时候,起始位置就从 j 开始到结束,将剩下的这段区域内的元素全部置为 0。 动画演示:
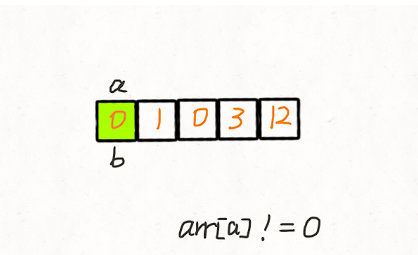
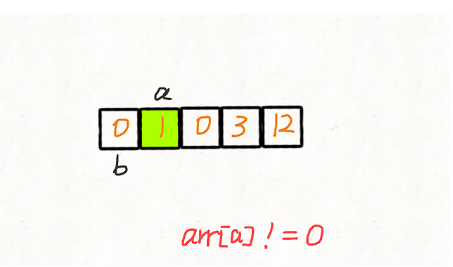
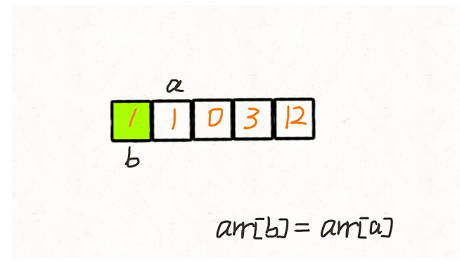
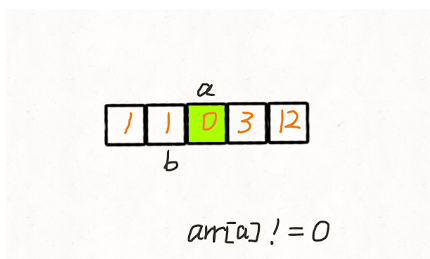
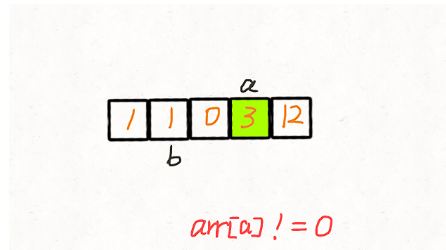
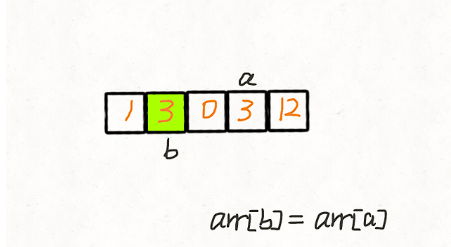
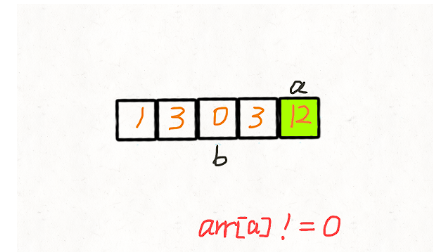
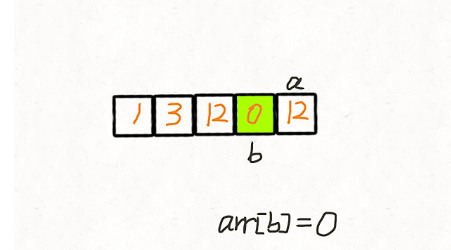
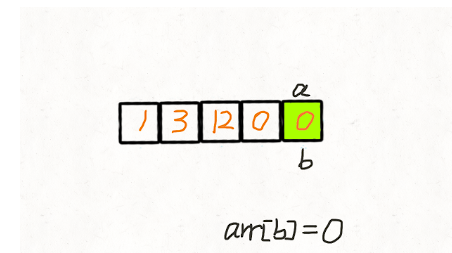
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public void moveZeroes(int[] nums) {
if(nums==null) {
return;
}
//第一次遍历的时候,j指针记录非0的个数,只要是非0的统统都赋给nums[j]
int j = 0;
for(int i=0;i<nums.length;++i) {
if(nums[i]!=0) {
nums[j++] = nums[i];
}
}
//非0元素统计完了,剩下的都是0了
//所以第二次遍历把末尾的元素都赋为0即可
for(int i=j;i<nums.length;++i) {
nums[i] = 0;
}
}
}
时间复杂度:O(n) 空间复杂度:O(1)
双指针直接交换
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public void moveZeroes(int[] nums) {
if(nums==null) {
return;
}
//两个指针i和j
int j = 0;
for(int i=0;i<nums.length;i++) {
//当前元素!=0,就把其交换到左边,等于0的交换到右边
if(nums[i]!=0) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j++] = tmp;
}
}
}
}
时间复杂度:O(n) 空间复杂度:O(1)
2.盛最多水的容器
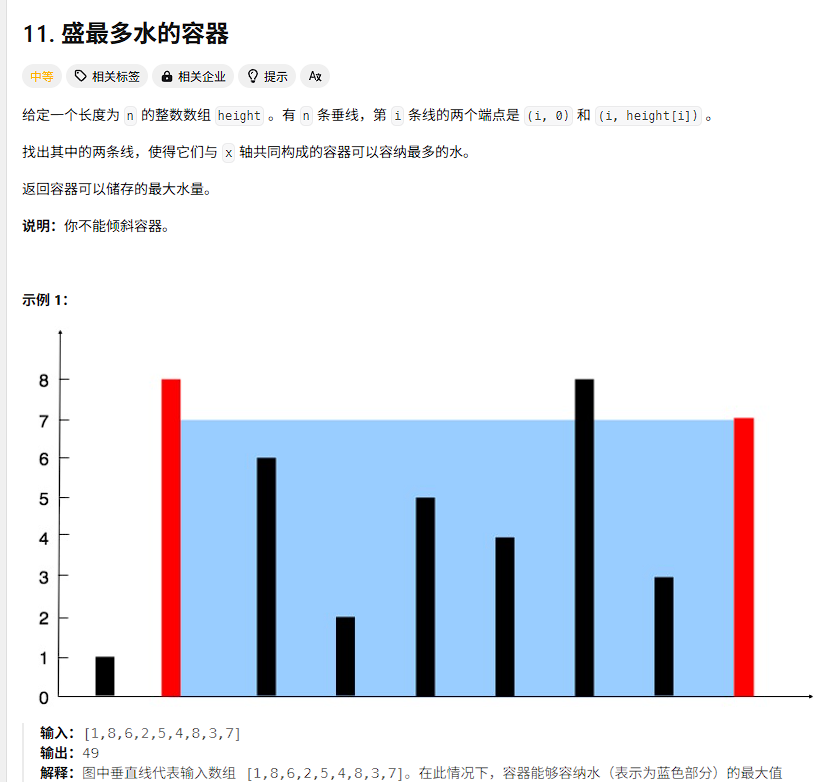

思路
设两指针 i , j ,指向的水槽板高度分别为 h[i] , h[j] ,此状态下水槽面积为 S(i,j) 。由于可容纳水的高度由两板中的 短板 决定,因此可得如下 面积公式 :
S(i,j)=min(h[i],h[j])×(j−i)
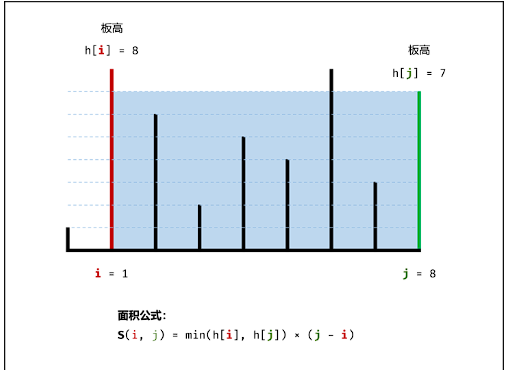
在每个状态下,无论长板或短板向中间收窄一格,都会导致水槽 底边宽度 −1 变短:
- 若向内 移动短板 ,水槽的短板 min(h[i],h[j]) 可能变大,因此下个水槽的面积 可能增大 。
- 若向内 移动长板 ,水槽的短板 min(h[i],h[j]) 不变或变小,因此下个水槽的面积 一定变小 。
因此,初始化双指针分列水槽左右两端,循环每轮将短板向内移动一格,并更新面积最大值,直到两指针相遇时跳出;即可获得最大面积。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public int maxArea(int[] height) {
int l = 0;
int r = height.length - 1;
int res = 0;
int area = 0;
while(l < r){
area = Math.min(height[l],height[r]) * (r - l);
res = Math.max(res,area);
if(height[l] < height[r]){
l++;
}else {
r--;
}
}
return res;
}
}
复杂度分析
- 时间复杂度 O(N) : 双指针遍历一次底边宽度 N 。
- 空间复杂度 O(1) : 变量 l , r , res,area 使用常数额外空间。
3.三数之和



解题思路
暴力法搜索为 O(N^2^) 时间复杂度,可通过双指针动态消去无效解来优化效率。
先将 nums 排序,时间复杂度为 O(NlogN)。
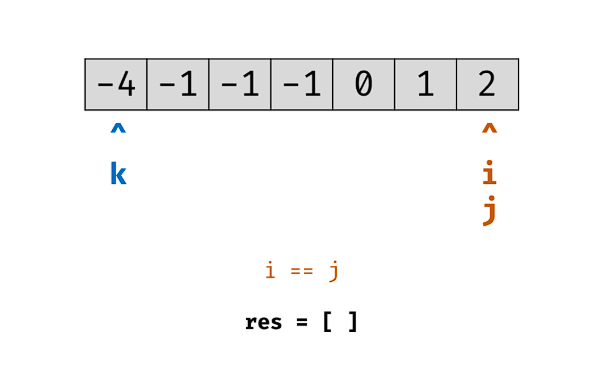
固定 3 个指针中最左(最小)元素的指针 k,双指针 i,j 分设在数组索引 (k,len(nums)) 两端。
双指针 i , j 交替向中间移动,记录对于每个固定指针 k 的所有满足 nums[k] + nums[i] + nums[j] == 0 的 i,j 组合:
1.当 nums[k] > 0 时直接 break 跳出:因为 nums[j] >= nums[i] >= nums[k] > 0,即 3 个元素都大于 0 ,在此固定指针 k 之后不可能再找到结果了。
2.当 k > 0且nums[k] == nums[k - 1]时即跳过此元素nums[k]:因为已经将 nums[k - 1] 的所有组合加入到结果中,本次双指针搜索只会得到重复组合。 3.i,j 分设在数组索引 (k,len(nums)) 两端,当i < j时循环计算s = nums[k] + nums[i] + nums[j],并按照以下规则执行双指针移动:
- 当
s < 0时,i += 1并跳过所有重复的nums[i]; - 当
s > 0时,j -= 1并跳过所有重复的nums[j]; - 当
s == 0时,记录组合[k, i, j]至res,执行i += 1和j -= 1并跳过所有重复的nums[i]和nums[j],防止记录到重复组合。









代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
//排序
Arrays.sort(nums);
List<List<Integer>> res = new ArrayList<>();
for (int k = 0; k < nums.length - 2; k++) {
//后面为递增的,结果不可能为0,直接结束
if(nums[k] > 0){
break;
}
//对k去重
if(k > 0 && nums[k] == nums[k - 1]){
continue;
}
int i = k + 1;
int j = nums.length - 1;
while(i < j){
int target = -nums[k];
if(nums[i] + nums[j] < target){
//需要变大,i右移并去重
while(i < j && nums[i] == nums[++i]);
}else if(nums[i] + nums[j] > target){
//需要变小,j左移并去重
while(i < j && nums[j] == nums[--j]);
}else {
//满足结果
res.add(new ArrayList<Integer>(Arrays.asList(nums[k],nums[i],nums[j])));
//i继续右移,j继续左移,同时去重
while(i < j && nums[i] == nums[++i]);
while(i < j && nums[j] == nums[--j]);
}
}
}
return res;
}
}
复杂度分析
- 时间复杂度 O(N^2^):其中固定指针
k循环复杂度 O(N),双指针i,j复杂度 O(N)。 - 空间复杂度 O(1):指针使用常数大小的额外空间。
4.接雨水

思路
求每一列的水,我们只需要关注当前列,以及左边最高的墙,右边最高的墙就够了。
装水的多少,当然根据木桶效应,我们只需要看左边最高的墙和右边最高的墙中较矮的一个就够了。
所以,根据较矮的那个墙和当前列的墙的高度可以分为三种情况。
-
较矮的墙的高度大于当前列的墙的高度
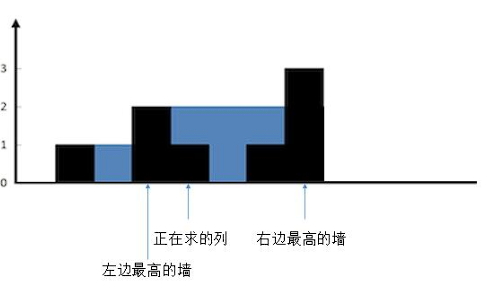
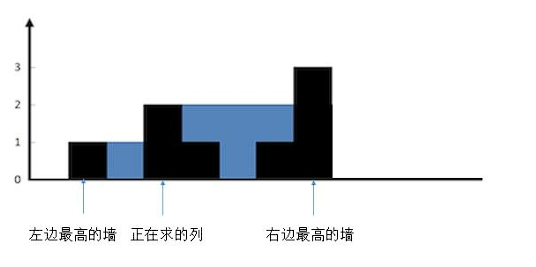
这样就很清楚了,现在想象一下,往两边最高的墙之间注水。正在求的列会有多少水?
很明显,较矮的一边,也就是左边的墙的高度,减去当前列的高度就可以了,也就是 2 - 1 = 1,可以存一个单位的水。
-
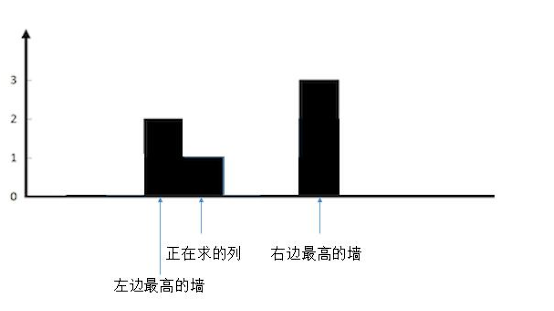
较矮的墙的高度小于当前列的墙的高度
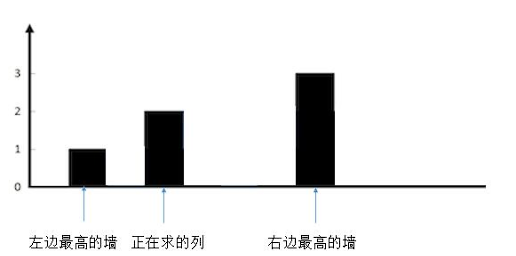
想象下,往两边最高的墙之间注水。正在求的列会有多少水?
正在求的列不会有水,因为它大于了两边较矮的墙。
-
较矮的墙的高度等于当前列的墙的高度
和上一种情况是一样的,不会有水。
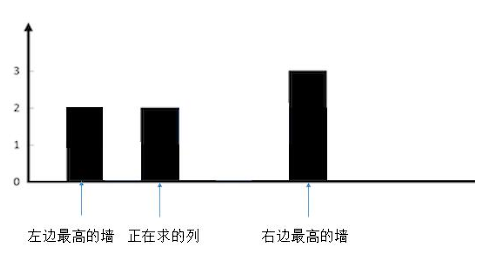
明白了这三种情况,程序就很好写了,遍历每一列,然后分别求出这一列两边最高的墙。找出较矮的一端,和当前列的高度比较,结果就是上边的三种情况。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public int trap(int[] height) {
int n = height.length;
int res = 0;
//左右指针
int left = 0,right = n - 1;
//左指针的左边最大高度、右指针的右边最大高度
int leftMax = height[left],rightMax = height[right];
// 最两边的列存不了水
left++;
right--;
// 向中间靠拢
while(left <= right){
leftMax = Math.max(leftMax,height[left]);
rightMax = Math.max(rightMax,height[right]);
if(leftMax < rightMax){
// 左指针的leftMax比右指针的rightMax矮
// 说明:左指针的右边至少有一个板子 > 左指针左边所有板子
// 根据水桶效应,保证了左指针当前列的水量决定权在左边
// 那么可以计算左指针当前列的水量:左边最大高度-当前列高度
res += leftMax - height[left];
left++;
}else {
// 右边同理
res += rightMax - height[right];
right--;
}
}
return res;
}
}
复杂度分析
- 时间复杂度 O(N)
- 空间复杂度 O(1)
总结

