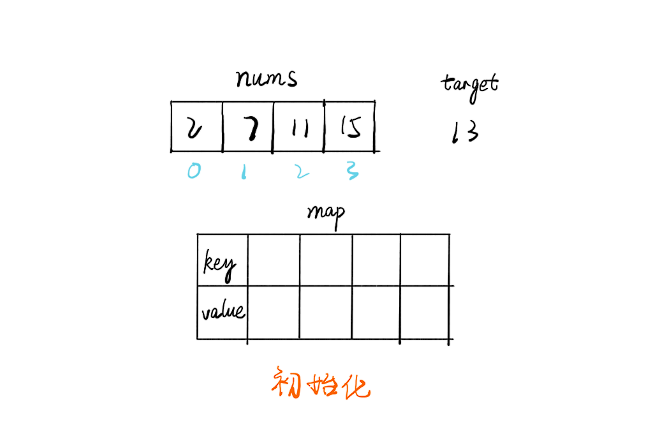
1.两数之和

思路
- 标签:哈希映射
- 这道题本身如果通过暴力遍历的话也是很容易解决的,时间复杂度在 O(n2)
- 由于哈希查找的时间复杂度为 O(1),所以可以利用哈希容器 map 降低时间复杂度
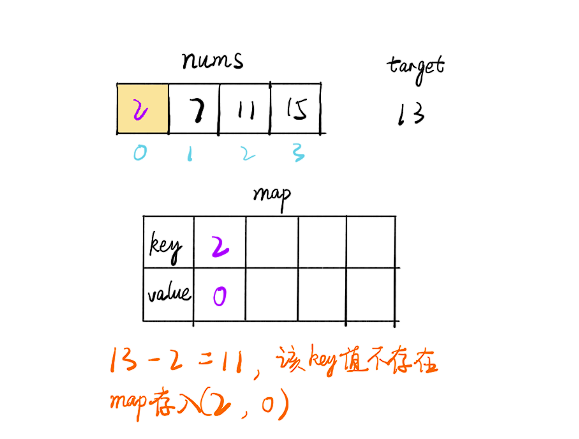
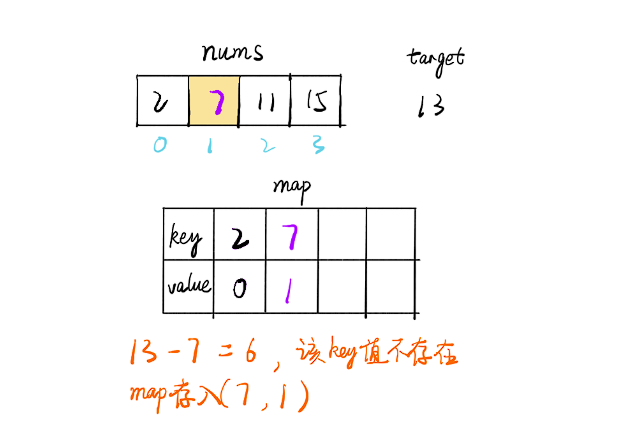
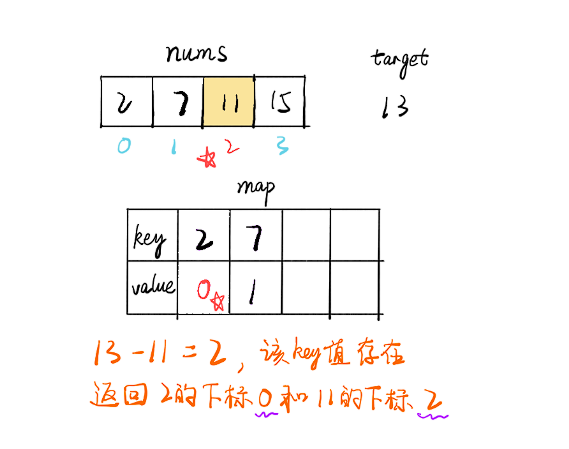
- 遍历数组 nums,i 为当前下标,每个值都判断 map 中是否存在 target-nums[i] 的 key 值
- 如果存在则找到了两个值,如果不存在则将当前的 (nums[i],i) 存入 map 中,继续遍历直到找到为止
- 如果最终都没有结果则抛出异常
- 时间复杂度:
O(n)
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public int[] twoSum(int[] nums, int target) {
Map<Integer,Integer> map = new HashMap<>(); //key为nums[i],value为i
for(int i = 0;i < nums.length;i++){
if(map.containsKey(target - nums[i])){
return new int[]{map.get(target-nums[i]),i};
}
map.put(nums[i],i);
}
throw new IllegalArgumentException("No two sum solution");
}
}
画解
2.字母异位词分组

题意解读
-
把每种字母出现次数都相同的字符串分到同一组。
-
例如 aab,aba,baa 可以分到同一组,但 abb 不行。
思路
-
注意到,如果把 aab,aba,baa 按照字母从小到大排序,我们可以得到同一个字符串 aab。
-
而对于每种字母出现次数不同于 aab 的字符串,例如 abb 和 bab,排序后为 abb,不等于 aab。
-
所以当且仅当两个字符串排序后一样,这两个字符串才能分到同一组。
-
根据这一点,我们可以用哈希表来分组,把排序后的字符串当作 key,原字符串组成的列表(即答案)当作 value。
-
最后把所有 value 加到一个列表中返回。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public List<List<String>> groupAnagrams(String[] strs) {
//key为排序后的字符串,value为原字符串组成的列表(即答案)
Map<String,List<String>> map = new HashMap<>();
for(String s : strs){
//把s排序,作为哈希表的key
char[] sortedS = s.toCharArray();
Arrays.sort(sortedS);
//排序后相同的字符串分到同一组
map.computeIfAbsent(new String(sortedS),k->new ArrayList<>()).add(s);
}
// 哈希表的 value 保存分组后的结果
return new ArrayList<>(map.values());
}
}
复杂度分析
- 时间复杂度:O(nmlogm),其中 n 为 strs 的长度,m 为 strs[i] 的长度。每个字符串排序需要 O(mlogm) 的时间。我们有 n 个字符串,所以总的时间复杂度为 O(nmlogm)。
- 空间复杂度:O(nm)。
补充
1
2
3
4
5
6
7
8
9
10
11
12
hashmap computeIfAbsent(K key, Function remappingFunction)
//key - 键
//remappingFunction - 重新映射函数,用于重新计算值
//返回值
//如果 key 对应的 value 不存在,则使用获取 remappingFunction 重新计算后的值,并保存为该 key 的 value,否则返回 value。
public char[] toCharArray()
//toCharArray() 方法将字符串转换为字符数组。
//参数无
//返回值字符数组
3.最长连续序列

核心思路
首先,本题是不能排序的,因为排序的时间复杂度是 O(nlogn),不符合题目 O(n) 的要求。
对于 nums 中的元素 x,以 x 为起点,不断查找下一个数 x+1,x+2,⋯ 是否在 nums 中,并统计序列的长度。
为了做到 O(n) 的时间复杂度,需要两个关键优化:
- 把 nums 中的数都放入一个哈希集合中,这样可以 O(1) 判断数字是否在 nums 中。
- 如果 x−1 在哈希集合中,则不以 x 为起点。为什么?因为以 x−1 为起点计算出的序列长度,一定比以 x 为起点计算出的序列长度要长!这样可以避免大量重复计算。比如 nums=[3,2,4,5],从 3 开始,我们可以找到 3,4,5 这个连续序列;而从 2 开始,我们可以找到 2,3,4,5 这个连续序列,一定比从 3 开始的序列更长。 ⚠ 注意:遍历元素的时候,要遍历哈希集合,而不是 nums!如果 nums=[1,1,1,…,1,2,3,4,5,…](前一半都是 1),遍历 nums 的做法会导致每个 1 都跑一个 O(n) 的循环,总的循环次数是 O(n2 ),会超时。

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public int longestConsecutive(int[] nums) {
HashSet<Integer> set = new HashSet<>();
for (int n : nums) {
set.add(n);
}
int count = 0;
int res = 0;
for (int n : set) {
if(!set.contains(n - 1)){
//说明这部分是开头的数据:头
count = 1;
int cur = n;
while(set.contains(cur + 1)){
//如果存在说明是:中
count++;
cur++;
}
//结束了说明到了:尾
res = Math.max(res,count);
}
}
return res;
}
}
复杂度分析
- 时间复杂度:O(n),其中 n 是 nums 的长度。在二重循环中,每个元素至多遍历两次:在外层循环中遍历一次,在内层循环中遍历一次。所以二重循环的时间复杂度是 O(n) 的。比如 nums=[1,2,3,4],其中 2,3,4 不会进入内层循环,只有 1 会进入内层循环。
- 空间复杂度:O(n)。
补充
-
HashSet 基于 HashMap 来实现的,是一个不允许有重复元素的集合。
-
HashSet 允许有 null 值。
-
HashSet 是无序的,即不会记录插入的顺序。
-
HashSet 不是线程安全的, 如果多个线程尝试同时修改 HashSet,则最终结果是不确定的。 您必须在多线程访问时显式同步对 HashSet 的并发访问。
- HashSet 实现了 Set 接口。
contains()方法是 Java 中HashSet类提供的一个常用方法,用于检查集合中是否包含指定的元素。该方法返回一个布尔值,表示元素是否存在。
总结

